Transformations in PyCairo

last modified July 17, 2023

In this part of the PyCairo graphics programming tutorial we talk about transformations.

An affine transform is composed of zero or more linear transformations (rotation, scaling or shear) and translation (shift). Several linear transformations can be combined into a single matrix. A rotation is a transformation that moves a rigid body around a fixed point. A scaling is a transformation that enlarges or diminishes objects. The scale factor is the same in all directions. A translation is a transformation that moves every point a constant distance in a specified direction. A shear is a transformation that moves an object perpendicular to a given axis, with greater value on one side of the axis than the other.

Translation

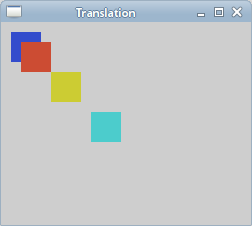
The following example describes a simple translation.

def on_draw(self, wid, cr):

    cr.set_source_rgb(0.2, 0.3, 0.8)
    cr.rectangle(10, 10, 30, 30)
    cr.fill()

    cr.translate(20, 20)
    cr.set_source_rgb(0.8, 0.3, 0.2)
    cr.rectangle(0, 0, 30, 30)
    cr.fill()

    cr.translate(30, 30)
    cr.set_source_rgb(0.8, 0.8, 0.2)
    cr.rectangle(0, 0, 30, 30)
    cr.fill()

    cr.translate(40, 40)
    cr.set_source_rgb(0.3, 0.8, 0.8)
    cr.rectangle(0, 0, 30, 30)
    cr.fill()

The example draws a rectangle. Then we do a translation and draw the same rectangle again a few times.

cr.translate(20, 20)

The translate function modifies the current transformation matrix by translating the user space origin. In our case we shift the origin by 20 units in both directions.

Shearing

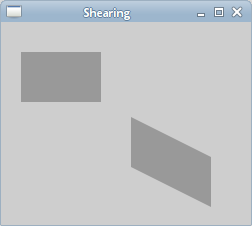
In the following example, we perform a shearing operation. A shearing is an object distortion along a particular axis. There is no shear method for this operation. We need to create our own transformation matrix. Note that each affine transformation can be performed by creating a transformation matrix.

def on_draw(self, wid, cr):

    cr.set_source_rgb(0.6, 0.6, 0.6)
    cr.rectangle(20, 30, 80, 50)
    cr.fill()

    mtx = cairo.Matrix(1.0, 0.5,
                0.0, 1.0,
                0.0, 0.0)

    cr.transform(mtx)
    cr.rectangle(130, 30, 80, 50)
    cr.fill()

In this code example, we perform a simple shearing operation.

mtx = cairo.Matrix(1.0, 0.5,
            0.0, 1.0,
            0.0, 0.0)

This transformation shears y values by 0.5 of the x values.

cr.transform(mtx)

We perform the transformation with the transform method.

Scaling

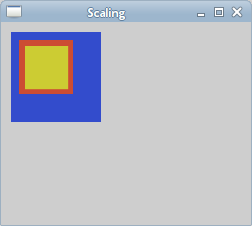
The next example demonstrates a scaling operation. Scaling is a transformation operation where the object is enlarged or shrunken.

def on_draw(self, wid, cr):

    cr.set_source_rgb(0.2, 0.3, 0.8)
    cr.rectangle(10, 10, 90, 90)
    cr.fill()

    cr.scale(0.6, 0.6)
    cr.set_source_rgb(0.8, 0.3, 0.2)
    cr.rectangle(30, 30, 90, 90)
    cr.fill()

    cr.scale(0.8, 0.8)
    cr.set_source_rgb(0.8, 0.8, 0.2)
    cr.rectangle(50, 50, 90, 90)
    cr.fill()

We draw three rectangles of 90x90px size. On two of them, we perform a scaling operation.

cr.scale(0.6, 0.6)
cr.set_source_rgb(0.8, 0.3, 0.2)
cr.rectangle(30, 30, 90, 90)
cr.fill()

We uniformly scale a rectangle by a factor of 0.6.

cr.scale(0.8, 0.8)
cr.set_source_rgb(0.8, 0.8, 0.2)
cr.rectangle(50, 50, 90, 90)
cr.fill()

Here we perform another scaling operation by a factor of 0.8. If we look at the picture, we can see that the third yellow rectangle is the smallest one. Even if we have used a smaller scaling factor. This is because transformation operations are additive. In fact, the third rectangle was scaled by a factor of 0.528 (0.6x0.8).

Isolating transformations

Transformation operations are additive. To isolate one operation from the other one, we can use the save and restore methods. The save method makes a copy of the current state of the drawing context and saves it on an internal stack of saved states. The restore method will re-establish the context to the saved state.

def on_draw(self, wid, cr):

    cr.set_source_rgb(0.2, 0.3, 0.8)
    cr.rectangle(10, 10, 90, 90)
    cr.fill()

    cr.save()
    cr.scale(0.6, 0.6)
    cr.set_source_rgb(0.8, 0.3, 0.2)
    cr.rectangle(30, 30, 90, 90)
    cr.fill()
    cr.restore()

    cr.save()
    cr.scale(0.8, 0.8)
    cr.set_source_rgb(0.8, 0.8, 0.2)
    cr.rectangle(50, 50, 90, 90)
    cr.fill()
    cr.restore()

In the example we scale two rectangles. This time we isolate the scaling operations from each other.

cr.save()
cr.scale(0.6, 0.6)
cr.set_source_rgb(0.8, 0.3, 0.2)
cr.rectangle(30, 30, 90, 90)
cr.fill()
cr.restore()

We isolate the scaling operation by putting the scale method between the save and restore methods.

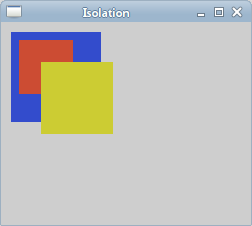
Now the third yellow rectangle is bigger than the second red one.

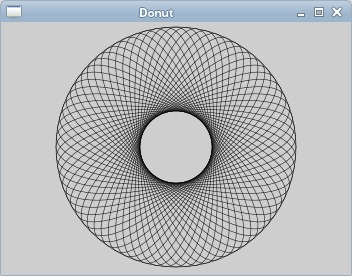
Donut

In the following example we create a complex shape by rotating a bunch of ellipses.

#!/usr/bin/python

'''
ZetCode PyCairo tutorial

This program creates a 'donut' shape
in PyCairo.

author: Jan Bodnar
website: zetcode.com
'''


from gi.repository import Gtk
import cairo
import math


class Example(Gtk.Window):

    def __init__(self):
        super(Example, self).__init__()

        self.init_ui()


    def init_ui(self):

        darea = Gtk.DrawingArea()
        darea.connect("draw", self.on_draw)
        self.add(darea)

        self.set_title("Donut")
        self.resize(350, 250)
        self.set_position(Gtk.WindowPosition.CENTER)
        self.connect("delete-event", Gtk.main_quit)
        self.show_all()


    def on_draw(self, wid, cr):

        cr.set_line_width(0.5)

        w, h = self.get_size()

        cr.translate(w/2, h/2)
        cr.arc(0, 0, 120, 0, 2*math.pi)
        cr.stroke()

        for i in range(36):
            cr.save()
            cr.rotate(i*math.pi/36)
            cr.scale(0.3, 1)
            cr.arc(0, 0, 120, 0, 2*math.pi)
            cr.restore()
            cr.stroke()


def main():

    app = Example()
    Gtk.main()


if __name__ == "__main__":
    main()

We do rotation and scaling operations. We also save and restore PyCairo contexts.

cr.translate(w/2, h/2)
cr.arc(0, 0, 120, 0, 2*math.pi)
cr.stroke()

In the middle of the GTK window, we create a circle. This will be a bounding circle for our ellipses.

for i in range(36):
    cr.save()
    cr.rotate(i*math.pi/36)
    cr.scale(0.3, 1)
    cr.arc(0, 0, 120, 0, 2*math.pi)
    cr.restore()
    cr.stroke()

We create 36 ellipses along the path of our bounding circle. We insulate each rotate and scale operation from one another with the save and restore methods.

Star

The next example shows a rotating and scaling star.

#!/usr/bin/python

'''
ZetCode PyCairo tutorial

This is a star example which
demonstrates scaling, translating and
rotating operations in PyCairo.

author: Jan Bodnar
website: zetcode.com
'''


from gi.repository import Gtk, GLib
import cairo


class cv(object):

    points = (
        ( 0, 85 ),
        ( 75, 75 ),
        ( 100, 10 ),
        ( 125, 75 ),
        ( 200, 85 ),
        ( 150, 125 ),
        ( 160, 190 ),
        ( 100, 150 ),
        ( 40, 190 ),
        ( 50, 125 ),
        ( 0, 85 )
    )

    SPEED = 20
    TIMER_ID = 1


class Example(Gtk.Window):

    def __init__(self):
        super(Example, self).__init__()

        self.init_ui()
        self.init_vars()


    def init_ui(self):

        self.darea = Gtk.DrawingArea()
        self.darea.connect("draw", self.on_draw)
        self.add(self.darea)

        self.set_title("Star")
        self.resize(400, 300)
        self.set_position(Gtk.WindowPosition.CENTER)
        self.connect("delete-event", Gtk.main_quit)
        self.show_all()


    def init_vars(self):

        self.angle = 0
        self.scale = 1
        self.delta = 0.01

        GLib.timeout_add(cv.SPEED, self.on_timer)


    def on_timer(self):

        if self.scale < 0.01:
            self.delta = -self.delta

        elif self.scale > 0.99:
            self.delta = -self.delta

        self.scale += self.delta
        self.angle += 0.01

        self.darea.queue_draw()

        return True


    def on_draw(self, wid, cr):

        w, h = self.get_size()

        cr.set_source_rgb(0, 0.44, 0.7)
        cr.set_line_width(1)

        cr.translate(w/2, h/2)
        cr.rotate(self.angle)
        cr.scale(self.scale, self.scale)

        for i in range(10):
            cr.line_to(cv.points[i][0], cv.points[i][1])

        cr.fill()


def main():

    app = Example()
    Gtk.main()


if __name__ == "__main__":
    main()

In this example, we create a star object. We translate it, rotate it and scale it.

points = (
    ( 0, 85 ),
    ( 75, 75 ),
    ( 100, 10 ),
    ( 125, 75 ),
    ( 200, 85 ),
...

The star object will be constructed from these points.

def init_vars(self):

    self.angle = 0
    self.scale = 1
    self.delta = 0.01
...

In the init_vars method, we initialize three variables. The self.angle is used in the rotation, the self.scale in scaling the star object. The self.delta variable controls when the star is growing and when it is shrinking.

glib.timeout_add(cv.SPEED, self.on_timer)

Each cv.SPEED ms the on_timer method is called.

if self.scale < 0.01:
    self.delta = -self.delta

elif self.scale > 0.99:
    self.delta = -self.delta

These lines control whether the star is going to grow or shrink.

cr.translate(w/2, h/2)
cr.rotate(self.angle)
cr.scale(self.scale, self.scale)

We shift the star into the middle of the window. Rotate it and scale it.

for i in range(10):
    cr.line_to(cv.points[i][0], cv.points[i][1])

cr.fill()

Here we draw the star object.

In this part of the PyCairo tutorial, we talked about transformations.