Transformations in HTML5 canvas

last modified July 17, 2023

In this part of the HTML5 canvas tutorial we talk about transformations.

An affine transform is composed of zero or more linear transformations (rotation, scaling, or shear) and translation (shift). Several linear transformations can be combined into a single matrix. A rotation is a transformation that moves a rigid body around a fixed point. A scaling is a transformation that enlarges or diminishes objects. The scale factor is the same in all directions. A translation is a transformation that moves every point a constant distance in a specified direction. A shear is a transformation that moves an object perpendicular to a given axis, with greater value on one side of the axis than the other.

There is a transform method, which multiplies the current transformation with the matrix described by the arguments of the method. We are able to scale, rotate, move, and shear the context. There are also methods that perform specific transformations: translate, rotate, and scale.

Translation

The following example shows a simple translation.

translation.html

<!DOCTYPE html>
<html>
<head>
<title>HTML5 canvas translation</title>
<style>
    canvas {border: 1px solid #bbbbbb}
</style>    
<script>
    function draw() {
        var canvas = document.getElementById('myCanvas');
        var ctx = canvas.getContext('2d');
    
        ctx.fillStyle = 'gray';
        ctx.translate(canvas.width/2, canvas.height/2);
        ctx.beginPath();
        ctx.arc(0, 0, 30, 0, 2*Math.PI);
        ctx.fill();
    }    
</script>
</head>
    
<body onload="draw();">
    <canvas id="myCanvas" width="150" height="150">
    </canvas>
</body>
</html>

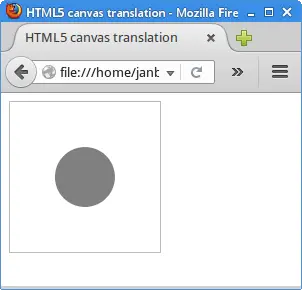
The example draws a circle in the middle of the canvas.

ctx.translate(canvas.width/2, canvas.height/2);

The translate method moves the origin of the coordinate system into the middle of the canvas.

ctx.beginPath();
ctx.arc(0, 0, 30, 0, 2*Math.PI);
ctx.fill();

A circle is drawn. Its center point is the middle of the canvas.

Rotation

The next example demonstrates a rotation.

rotation.html

<!DOCTYPE html>
<html>
<head>
<title>HTML5 canvas rotation</title>
<script>
    function draw() {
        var canvas = document.getElementById('myCanvas');
        var ctx = canvas.getContext('2d');
    
        ctx.fillStyle = 'gray';
        ctx.rotate(Math.PI/10);
        ctx.fillRect(50, 10, 120, 80);
    }    
</script>
</head>
    
<body onload="draw();">
    <canvas id="myCanvas" width="200" height="200">
    </canvas>
</body>
</html>

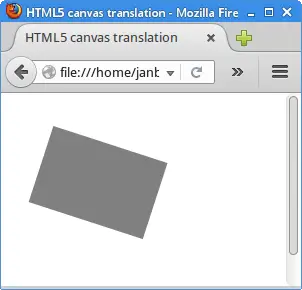
The example performs a rotation on a rectangle.

ctx.rotate(Math.PI/10);

The rotate method performs rotation. The angle argument represents a clockwise rotation angle and is expressed in radians.

Scaling

Scaling is done with the scale method. The method takes two parameters: x scale factor and y scale factor.

scaling.html

<!DOCTYPE html>
<html>
<head>
<title>HTML5 canvas scaling</title>
<script>
    function draw() {
        var canvas = document.getElementById('myCanvas');
        var ctx = canvas.getContext('2d');
    
        ctx.fillStyle = 'gray';
        ctx.fillRect(20, 20, 80, 50);

        ctx.save();
        ctx.translate(110, 22);
        ctx.scale(0.5, 0.5);
        ctx.fillRect(0, 0, 80, 50);
        ctx.restore();

        ctx.translate(170, 20);
        ctx.scale(1.5, 1.5);
        ctx.fillRect(0, 0, 80, 50);
    }    
</script>
</head>
    
<body onload="draw();">
    <canvas id="myCanvas" width="300" height="200">
    </canvas>
</body>
</html>

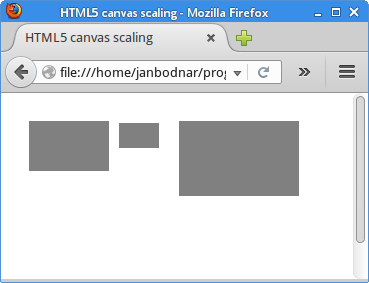
In the example, there is a rectangle object. First, we scale it down and then we scale it up a bit.

ctx.save();
ctx.translate(110, 22);
ctx.scale(0.5, 0.5);
ctx.fillRect(0, 0, 80, 50);
ctx.restore();

The transformation operations are additive. In order to isolate the translation and scaling operations, we place them between save and restore methods. The save method saves the entire state of the canvas and the restore method restores it.

Shearing

A shear is a transformation that distorts the shape of an object along either or both of the axes. Like scale and translate, a shear can be done along just one or along both of the coordinate axes.

shearing.html

<!DOCTYPE html>
<html>
<head>
<title>HTML5 canvas shearing</title>
<script>
    function draw() {
        var canvas = document.getElementById('myCanvas');
        var ctx = canvas.getContext('2d');
        
        ctx.translate(0.5, 0.5);
        ctx.setLineDash([2]);
        
        ctx.save();
        ctx.strokeStyle = 'green';
        ctx.strokeRect(50, 90, 160, 50);
        ctx.restore();
        
        ctx.save();
        ctx.strokeStyle = 'blue';
        ctx.transform(1, 1, 0, 1, 0, 0);
        ctx.strokeRect(50, 40, 80, 50);
        ctx.restore();
        
        ctx.save();
        ctx.strokeStyle = 'red';
        ctx.transform(1, 1, 0, 1, 0, -130);
        ctx.strokeRect(130, 10, 80, 50);
        ctx.restore();        
    }    
</script>
</head>
    
<body onload="draw();">
    <canvas id="myCanvas" width="300" height="300">
    </canvas>
</body>
</html>

There is not a specifiec method for shearing, we use the generic transform method.

ctx.translate(0.5, 0.5);

This line makes the lines of the rectangles smoother.

ctx.save();
ctx.strokeStyle = 'blue';
ctx.transform(1, 1, 0, 1, 0, 0);
ctx.strokeRect(50, 40, 80, 50);
ctx.restore();

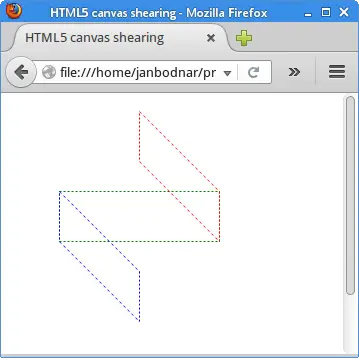
The blue rectangle is horizontally sheared (skewed). The parameters of the transform method are: horizontal scaling, horizontal shearing, vertical shearing, vertical scaling, horizontal translation, and vertical translation.

Donut

In the following example we create an complex shape by rotating an ellipse.

donut.html

<!DOCTYPE html>
<html>
<head>
<title>HTML5 canvas donut</title>
<script>
    function draw() {
        var canvas = document.getElementById('myCanvas');
        var ctx = canvas.getContext('2d');
    
        ctx.fillStyle = 'gray';
        ctx.translate(0.5, 0.5);
        
        var x = canvas.width/2;
        var y = canvas.height/2;

        for (var deg = 0; deg < 360; deg += 5) {
            
            var rad = deg * Math.PI / 180; 
            ctx.beginPath();
            ctx.ellipse(x, y, 30, 130, rad, 0, 2*Math.PI);
            ctx.stroke();
        }
    }    
</script>
</head>
    
<body onload="draw();">
    <canvas id="myCanvas" width="300" height="300">
    </canvas>
</body>
</html>

The example uses the ellipse method, which at the moment of writing this tutorial, is not supported by all browers. The example runs on Chrome and Opera.

var x = canvas.width/2;
var y = canvas.height/2;

The ellipse's center point is located in the center of the canvas.

for (var deg = 0; deg < 360; deg += 5) {
    
    var rad = deg * Math.PI / 180; 
    ctx.beginPath();
    ctx.ellipse(x, y, 30, 130, rad, 0, 2*Math.PI);
    ctx.stroke();
}

We create 36 ellipses. The ellipses are rotated. The ellipse method takes the following parameters: the x and y coordinates of the ellipse's center point, the ellipse's major axis radius, the ellipse's minor axis radius, rotation, start angle, and end angle.